Cuestionario

Cuestionario II Quimestre.

1. Ingresar a Schoology.
2. Ingresar Código (Access Code): CQSDXVMWMB7NZ.
3. Crearse una cuenta.
4. Relizar los cuestionarios.

Link:

https://app.schoology.com/register.php?type=student

Access Code 1 BGU:

CQSDXVMWMB7NZ

Operaciones con Funciones

Operaciones con Funciones

Las funciones con dominios que se traslapan pueden ser sumadas, restadas, multiplicadas y divididas. Si f ( x ) y g ( x ) son dos funciones, entonces para todas las x en el dominio de ambas funciones la suma, diferencia, producto y cociente están definidos como sigue.

      ( f + g )( x ) = f ( x ) + g ( x )

      ( f – g )( x ) = f ( x ) – g ( x )

      ( fg )( x ) = f ( x ) × g ( x )

      

Ejemplo :

Digamos que f ( x ) = 2 x + 1 y g ( x ) = x 2 – 4. 

Encuentre ( f + g )( x ), ( f – g )( x ), ( fg )( x ) y  .

( f + g )( x ) = f ( x ) + g ( x )

          = (2 x + 1) + ( x 2 – 4)

          = x 2 + 2 x – 3

( f – g )( x ) = f ( x ) – g ( x )

         = (2 x + 1) – ( x 2 – 4)

         = – x 2 + 2 x + 5

( fg )( x ) = f ( x ) × g ( x )    

     = (2 x + 1)( x 2 – 4)

     = 2 x 3 + x 2 – 8 x – 4 

Otra forma de combinar dos funciones para crear una nueva función es llamada la composición de funciones . En la composición de funciones sustituimos una función completa en otra función.

La notación de la función f con g es  y se lee f de g de x . Significa que donde sea que haya una x en la función f , es reemplazada con la función g ( x ). El dominio de  es el conjunto de todas las x en el dominio de g tal que g ( x ) está en el dominio de f .

Ejemplo 1:

Digamos que f ( x ) = x 2 y g ( x ) = x – 3. Encuentre f ( g ( x )).

Ejemplo 2:

Digamos que f ( x ) = 2 x – 1 y g ( x ) = x + 2. Encuentre f ( g ( x )).

El orden SI importa cuando encuentra la composición de funciones.

Ejemplo 3:

Digamos que f ( x ) = 3 x + 1 y g ( x ) = 2 x – 3. 

Encuentre f ( g ( x )) y g ( f ( x )).

Ya que 6 x – 8 ≠ 2 x – 1,    f ( g ( x )) ≠ g ( f ( x )).

Sistemas de Ecuaciones Cuadráticos

Sistemas de Ecuaciones Cuadráticos

Sistemas de Ecuaciones No Lineales

Objetivo de Aprendizaje

·         Resolver sistemas de ecuaciones lineales, cuadráticas y otras funciones no lineales.

Introducción

Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que comparten dos o más incógnitas. Las soluciones de un sistema de ecuaciones son todos los valores que son válidos para todas las ecuaciones, o los puntos donde las gráficas de las ecuaciones se intersectan.

Podemos resolver un sistema de ecuaciones lineales graficando, por sustitución y por combinación lineal. Los sistemas de funciones no lineales, como ecuaciones cuadráticas o exponenciales, pueden ser manejados con las mismas técnicas.

Para ilustrar cómo resolver estos sistemas, nos vamos a concentrar en sistemas lineales y cuadráticos con sólo dos ecuaciones. Pero ten en cuenta que hay sistemas que pueden ser más grandes y más complejos que estos ejemplos.

Sistemas de Ecuaciones Lineales y Cuadráticas

Empecemos por hablar sobre dos ecuaciones lineales. La solución de este tipo de sistema es el punto de intersección entre las dos rectas, o el lugar donde las dos ecuaciones tienen los mismos valores de x y de y. Puede haber más de una solución, no solución, o un número infinito de soluciones de un sistema de dos ecuaciones lineales:

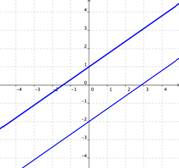
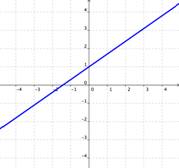
Una solución	No hay solución	Soluciones infinitas
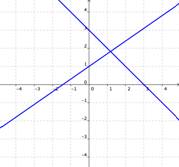Si las gráficas de las ecuaciones se intersectan, entonces existe una solución para ambas ecuaciones.	Si las gráficas de dos ecuaciones no se intersectan (por ejemplo, si son paralelas), entonces no existen soluciones para ambas ecuaciones.	Si las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones para ambas ecuaciones.

Para resolver un sistema con una ecuación lineal y una ecuación cuadrática, podemos hacer lo mismo, encontrar el punto — o puntos — de intersección entre ambas gráficas:

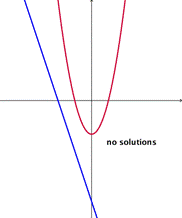
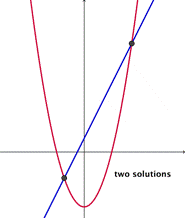
Una solución	No hay solución	Dos soluciones
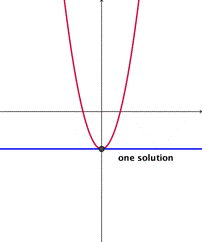Si la parábola y la recta se tocan en un sólo punto, entonces existe una solución para ambas ecuaciones.	Si las gráficas de las ecuaciones no se intersectan, entonces no existen soluciones para ambas ecuaciones.	Si la recta se intersecta con la parábola en dos lugares, entonces hay dos soluciones para ambas ecuaciones.

No tiene sentido considerar el caso cuando las dos ecuaciones representan el mismo conjunto de puntos, porque una línea recta jamás será una parábola, y vice versa.

Nota que esto significa que el número posible de soluciones para un sistema de dos ecuaciones lineales es 0 (nunca se tocan), 1 (se cruzan en un lugar), o infinito (las rectas son idénticas). El número de soluciones para un sistema con una ecuación lineal y una ecuación cuadrática es 0 (nunca se tocan), 1 (se tocan en un lugar), o 2 (se cruzan en dos lugares).

Vamos a resolver por medio de gráficas un sistema de una ecuación lineal y una ecuación cuadrática.

Ejemplos
Problema	Resolver el sistema graficando las ecuaciones       y
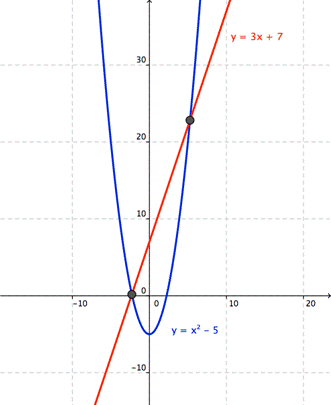			Graficar cada ecuación y localizar los puntos de intersección
Solución	Este sistema tiene dos soluciones, No podemos determinar la posición exacta de los puntos de intersección a partir de la gráfica, pero son aproximadamente (-2,0) y (5,22)

Nota que a pesar de que podemos saber aproximadamente donde se intersectan las gráficas, es difícil encontrar la posición exacta.

Ahora vamos a resolver el mismo sistema usando sustitución. Cuando resolvemos por sustitución, seguimos los siguientes pasos: 

1. Seleccionar una ecuación y despejar una variable. (Escoger una ecuación y una variable que sea fácil de despejar).
2. Sustituir la expresión resultante por una variable en la otra ecuación, cada vez que esta variable aparezca.
3. Resolver la segunda variable en la segunda ecuación.
4. Sustituir la solución del paso 3 en la expresión del paso 1, para encontrar la otra variable.

Ejemplo
Problema	Resolver el sistema usando el método de sustitución  y
				En este caso, ambas ecuaciones tienen la variable y despejada, por lo que las podemos igualar
				Restar 3x de ambos lados y restar 7 de ambos lados.  Ahora queda una ecuación cuadrática igual a 0 por lo que podemos usar la fórmula cuadrática, , para encontrar la solución
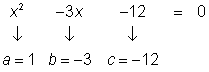				a = 1,  b = -3, y c = -12
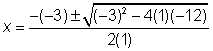				Sustituir los valores de a, b, y c en la fórmula
				Simplificar
o				Simplificar un poco más, recordando evaluar ambos  y .
				Evaluar cualquiera de las funciones con cada x para encontrar el valor de y correspondiente
Solución	(5.27, 22.82) y (-2.27, 0.18)

Usando sustitución hemos llegado a una respuesta más precisa que cuando lo hicimos graficando el sistema, sin embargo, si hicieron aproximaciones cuando sacamos la raíz cuadrada de 57. ¡Esta no es la solución exacta!

Es siempre buena idea comprobar el resultado en las ecuaciones originales.

Aquí hay una prueba con el punto (5.27, 22.82):

Nota que la comprobación no resulta en una igualdad perfecta, pero cercana.

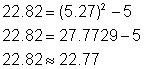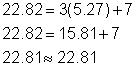Usar una gráfica para encontrar el número de soluciones del sistema de ecuaciones.                   y = -4x – 4 y y = -0.25x2 – 4 A) una solución B) dos soluciones C) no hay solución D) soluciones infinitas Mostrar/Ocultar la Respuesta

Sistemas de Dos Ecuaciones Cuadráticas

Ahora veamos el caso de dos ecuaciones cuadráticas. Imagina por un momento cómo las gráficas de las dos ecuaciones cuadráticas pueden intersectarse (o no).

Una solución	No hay solución
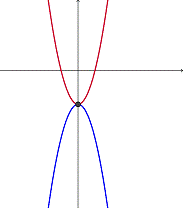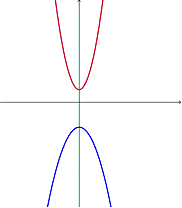Dos ecuaciones cuadráticas que tienen sólo un punto en común, como un vértice compartido, tienen una solución.	Dos ecuaciones cuadráticas que no se superponen (no tienen valores comunes de y) no tienen solución.
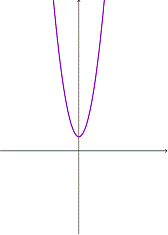
Dos soluciones	Soluciones infinitas
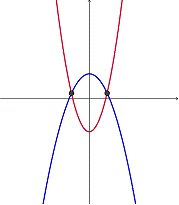Dos ecuaciones cuadráticas que se superponen pero tienen ecuaciones diferentes tienen dos soluciones	Si las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones válidas para ambas ecuaciones.

Podemos resolver el sistema de ecuaciones cuadráticas graficando:

Ejemplo
Problema	Resolver el sistema graficando las ecuaciones  y
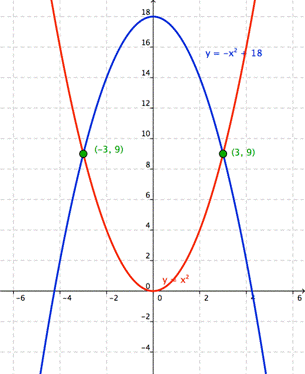			Graficar ambas ecuaciones y encontrar los puntos de intersección Aproximar las coordenadas de los puntos de intersección
Solución	(-3, 9)  y (3, 9)

Una vez más, no podemos estar seguros de que nuestras soluciones gráficas son exactas. Un método algebraico siempre puede garantizar una solución exacta. Por ejemplo, podemos resolver un sistema de ecuaciones cuadráticas por sustitución:

Ejemplo
Problema	Resolver el sistema usando el método de sustitución:  y
			En este caso ambas ecuaciones tienen la variable y despejada, por lo que las podemos igualar
			Sumar 2x2 y 6 a ambos lados para traer todas las variables a un lado de la ecuación
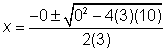			Aplicar la fórmula cuadrática.  a = 3, b = 0, y c = 10
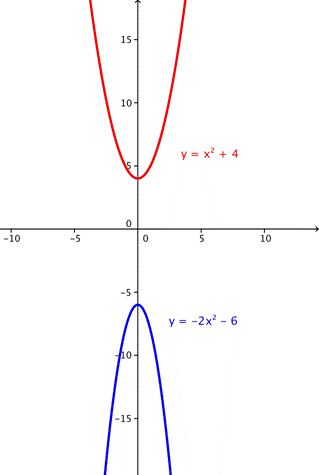
			Simplificar, notando que la cantidad debajo de la raíz cuadrada es un valor negativo - este es el [discriminante] - lo que significa que no hay solución y las gráficas no se intersectan
Solución	no hay solución

Como no hay solución, no podemos comprobar nuestra solución algebraicamente, pero podemos ver ambas gráficas para verificar que no hay solución:

También podemos usar combinación lineal para resolver sistemas de ecuaciones, siguiendo estos pasos:

1. Re arreglar las ecuaciones de forma que los términos se alineen.
2. Multiplicar ninguna, o una, o ambas ecuaciones por una constante para que los coeficientes de una de las variables sean opuestos.
3. Sumar las ecuaciones para eliminar una de las variables.
4. Resolver la ecuación resultante.
5. Sustituir la solución del paso 4 en la ecuación original para encontrar la otra variable.

¿Listo para intentarlo?

Ejemplo
Problema	Resolver el sistema usando combinación lineal  y
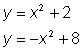			Alinear las ecuaciones
			Como ya hay dos variables que son opuestas (x2 y –x2), podemos sumar las dos ecuaciones
	y = 5		Despejar y dividiendo ambos lados de la ecuación entre 2
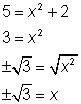			Sustituir y en una de las ecuaciones para encontrar los valores de x.
Solución	y

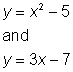
Resolver el sistema: Encontrar los puntos de intersección, si existen, de las dos ecuaciones siguientes: A) no hay solución, no hay puntos de intersección B)  C) (1,-4) y (2, -1) D) (-2, 13) y (-1, 4) Mostrar/Ocultar la Respuesta

Las mismas estrategias de graficar, sustitución, o combinación lineal pueden ser aplicadas para resolver sistemas de ecuaciones de otras funciones no lineales, como círculos, elipses, y otras funciones coordenadas.

Sumario

La solución de sistemas de ecuaciones no lineales puede hacerse usando las técnicas de graficar, sustitución y combinación lineal. De la misma forma que con sistemas de ecuaciones lineales, cuando encontramos soluciones a sistemas de ecuaciones no lineales, estamos buscando la intersección de sus gráficas o los lugares donde las ecuaciones tienen los mismos valores de las variables.